Il calcolo scientifico sta entrando in una fase in cui la domanda non è più soltanto “quanto veloce”, ma quanto sostenibile. Simulazioni ad alta risoluzione, mesh più dense, modelli fisici più ricchi e cicli di iterazione sempre più stretti stanno trasformando l’energia in un vincolo strutturale. In questo contesto, l’idea di spostare parte del carico numerico su hardware neuromorfo non è un esercizio di stile: è un tentativo di cambiare la fisica del computing, sostituendo un flusso di operazioni sincrone e costose con comunicazioni event-driven e parallelismo “nativo”. È esattamente la promessa che emerge dal lavoro di Bradley H. Theilman e James B. Aimone al Sandia National Laboratories, che mostrano come una piattaforma neuromorfica come Intel Loihi 2 possa risolvere sistemi lineari sparsi generati dal metodo degli elementi finiti (FEM). L’idea centrale è radicale nella sua semplicità: prendere la matematica di una discretizzazione FEM, trasformarla in una rete neurale spiking con connettività sparsa e far sì che la soluzione emerga come stato stazionario asincrono della dinamica neurale. Niente training, niente dataset, niente ottimizzazione “statistica” nel senso classico. Solo una mappatura diretta tra matrice sparsa e pesi sinaptici, tra termine noto e bias, tra vincoli di bordo e dinamiche del sistema.

Se funziona, l’impatto è doppio. Da un lato si ottiene un solutore che replica, con accuratezza numerica comparabile, ciò che già fanno solutori tradizionali. Dall’altro lo si ottiene con un profilo energetico compatibile con scenari che oggi sono difficili da immaginare su CPU e GPU: soluzioni ripetute, aggiornamenti rapidi, integrazione con sensori e stima continua, cioè un “gemello” che non si limita a simulare ma può seguire un sistema fisico in tempo quasi reale.
Da FEM a dinamica neurale: quando la matrice sparsa diventa una rete spiking
Il cuore dell’approccio chiamato NeuroFEM è la costruzione di una rete neurale spiking direttamente dalla struttura della matrice FEM. In un problema FEM classico, la discretizzazione di una PDE produce un sistema lineare del tipo A x = b, dove A è grande e sparsa, x è il vettore incognito e b incorpora sorgenti e vincoli. In NeuroFEM, ogni nodo della mesh viene associato a una piccola popolazione di neuroni ricorrenti, e l’architettura della rete riflette la geometria della mesh: densità locale (perché i nodi vicini sono accoppiati dagli elementi) e sparsità globale (perché non tutti i nodi interagiscono con tutti).
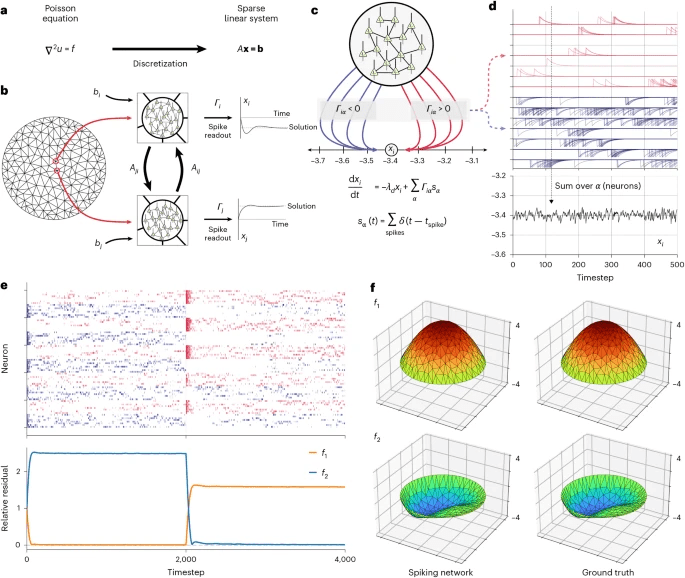
b , L’algoritmo neuromorfico agli elementi finiti (NeuroFEM) costruisce una SNN dal sistema lineare sparso. Ogni nodo della mesh nella discretizzazione contiene una popolazione di neuroni spiking. I pesi tra queste popolazioni neurali sono determinati dagli elementi della matrice del sistema lineare. Ogni popolazione riceve una distorsione determinata dal lato destro del sistema lineare. La costruzione della rete garantisce che la lettura dell’attività spiking fluisca alla soluzione del sistema lineare nel tempo.
c , I picchi dei neuroni all’interno di un singolo nodo della mesh, rappresentati come funzioni delta, proiettano su variabili di output con peso
Γ e vengono integrati tramite un’equazione differenziale ordinaria del primo ordine (in basso). Metà dei neuroni in un nodo proiettano con un peso di lettura positivo e metà con un peso negativo. Questo tiro alla fune tra neuroni con proiezione positiva e negativa porta la variabile di lettura al valore richiesto.
d , L’effetto dei singoli picchi è quello di aggiungere un kernel a decadimento esponenziale alla variabile di lettura. Le tracce rosse e blu indicano rispettivamente neuroni con pesi di lettura positivi e negativi. La somma di questi kernel su tutti i neuroni nel nodo fornisce una lettura fluttuante per la componente del sistema lineare corrispondente a questo nodo
e , NeuroFEM risolve sistemi lineari sparsi. L’attività di un circuito NeuroFEM costruito per risolvere l’equazione di Poisson su un disco fluisce verso le soluzioni rispetto a due diversi membri destri
La mappatura è diretta: i pesi sinaptici derivano dagli elementi della matrice del sistema, mentre i bias rappresentano il lato destro dell’equazione. La dinamica spiking implementa un sistema differenziale di primo ordine che, attraverso una sorta di “tiro alla fune” tra neuroni che rappresentano contributi positivi e negativi, spinge un valore di readout verso la soluzione corretta. Invece di iterare esplicitamente aggiornamenti di vettori e residui come in molti metodi numerici classici, la rete “si assesta” da sola, convergendo verso un regime asincrono stazionario.
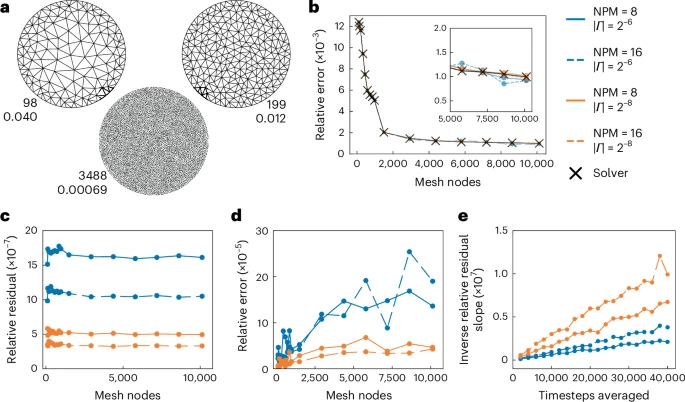
b , Sinistra: l’errore relativo rispetto alla soluzione analitica di NeuroFEM e a un risolutore convenzionale in funzione della risoluzione della mesh. Destra: legenda per tutti i pannelli.
c , Il residuo relativo del sistema lineare per punto della mesh per NeuroFEM è costante in funzione del numero di nodi della mesh. Il residuo relativo viene migliorato aumentando il numero di neuroni per nodo della mesh e/o diminuendo l’ampiezza della lettura | Γ |.
d , L’errore relativo tra le soluzioni NeuroFEM e le soluzioni generate da un risolutore convenzionale.
e , Il residuo relativo migliora linearmente con il numero di intervalli di lettura mediati. La pendenza residua relativa inversa è definita come il reciproco del residuo relativo costante per nodo della mesh tracciato in
c . Curve più ripide indicano un miglioramento maggiore all’aumentare del numero di intervalli di tempo medi.
Qui c’è un dettaglio decisivo che distingue l’approccio da molta retorica sull’AI: la rete non sta imparando. Sta calcolando. La spiking neural network è un “circuito” che realizza una dinamica equivalente al problema numerico, e la soluzione è un punto fisso del sistema. Questo significa che cambiare il problema, entro certe classi, non implica necessariamente ricostruire tutto: gli autori descrivono come la modifica dei bias a runtime permetta di risolvere più istanze del sistema senza rifare da capo la rete, rendendo plausibile un uso iterativo o sensoriale.
Poisson su domini complessi: la prova di realtà per un solutore neuromorfo
La dimostrazione parte da un classico: l’equazione di Poisson su domini che possono includere geometrie non banali, fori e risoluzioni inhomogenee. È un banco di prova significativo perché Poisson è presente ovunque in fisica computazionale, e perché il comportamento numerico dei solutori si vede subito in termini di errori e residui. NeuroFEM viene valutato su mesh che crescono da poche centinaia fino a migliaia di nodi, con un meccanismo di media del readout dopo la convergenza per ridurre la variabilità intrinseca del regime spiking. La parte interessante non è solo che il metodo “arriva vicino” a un solutore tradizionale, ma che mostra un comportamento di errore coerente con la discretizzazione: l’errore relativo rispetto alla soluzione analitica decresce con la dimensione dell’elemento secondo una legge attesa, mentre il residuo relativo per nodo rimane controllato al crescere della mesh, se gli iperparametri vengono scelti in modo adeguato. La precisione, come in molti algoritmi numerici, non è gratis. Dipende da come si regola la rete: il numero di neuroni per nodo, la magnitudine del readout e il numero di timestep su cui si media dopo la convergenza. Ma il segnale è chiaro: non serve addestramento per ottenere una soluzione numericamente consistente. Serve ingegneria di iperparametri, che in un contesto FEM è un concetto familiare, perché ogni metodo numerico ha parametri, tolleranze e compromessi.
Rumore e asincronia: perché l’errore non è un bug, ma parte della stabilità
Un elemento controintuitivo ma cruciale è l’uso di rumore indipendente sui neuroni per bilanciare le dinamiche ed evitare sincronizzazioni indesiderate. In una rete spiking, la sincronizzazione può essere un problema: produce oscillazioni, peggiora la convergenza e rende instabile il readout. Il rumore, se calibrato, aiuta a mantenere un regime asincrono, facendo sì che la rete non collassi in stati collettivi “rigidi” ma rimanga in una dinamica che, in media, converge alla soluzione. Questo punto è importante perché avvicina l’algoritmo a una logica neurobiologica: circuiti corticali reali operano in regimi di attività irregolare e asincrona, e proprio questa irregolarità è spesso interpretata come un vantaggio per la robustezza. In NeuroFEM, la stessa idea diventa numerica: l’asincronia è una proprietà funzionale che consente alla rete di rappresentare un equilibrio computazionale stabile.
Dalle PDE scalari alle PDE vettoriali: elasticità lineare in 3D e mesh irregolari
Se Poisson è la porta d’ingresso, la vera dimostrazione di ambizione è l’estensione a problemi più complessi, come l’elasticità lineare in tre dimensioni e mesh tetraedriche irregolari. Qui la dimensione del sistema cresce rapidamente e la struttura delle matrici diventa ancora più articolata. Il lavoro descrive un caso con centinaia di elementi che genera una matrice di dimensioni nell’ordine di migliaia per migliaia, risolta con una rete che usa più neuroni per nodo per rappresentare il campo vettoriale di spostamento. L’elemento che rende credibile l’approccio è la fedeltà numerica: le differenze rispetto a solutori convenzionali restano contenute entro bound indicati e non esplodono con la dimensione del problema. In altre parole, il metodo non appare come un “trucco” valido per un caso toy, ma come un paradigma trasferibile a classi di problemi FEM reali, a patto di gestire con cura iperparametri, precisione e scaling. E c’è un aspetto operativo che conta più dei numeri: l’integrazione con tool FEM esistenti. L’uso di pipeline che passano da strumenti di mesh e assembly già diffusi riduce la barriera di adozione. È un punto spesso ignorato quando si parla di hardware alternativo: anche un’idea eccellente fallisce se richiede di riscrivere anni di toolchain. Qui, invece, l’obiettivo dichiarato è far sì che chi fa FEM possa importare il proprio lavoro e “girarlo” su neuromorfo senza cambiare mentalità.
Loihi 2 e la realtà del fixed-point: accuratezza stabile, ma con cicatrici numeriche
Portare un algoritmo su hardware neuromorfo non significa soltanto “eseguirlo più efficiente”. Significa confrontarsi con vincoli concreti: rappresentazioni fixed-point, pesi sinaptici a bit limitati, range dinamico e quantizzazione. Su Loihi 2 vengono citati pesi sinaptici a 8 bit e stati a 24 bit, con una riscalatura dei parametri in potenze di due per allinearsi a bit-shift e ridurre errori.
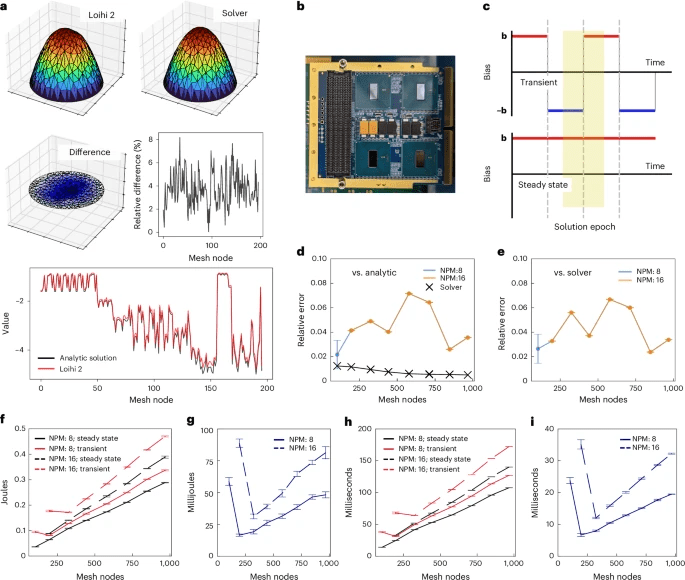
b , La scheda Loihi 2 Oheo Gulch utilizzata per questo studio. Ogni scheda ha otto chip (quattro in alto e quattro in basso) e il sistema completo è costituito da una pila di quattro schede. I nostri studi di profilazione sono stati limitati a un singolo chip.
c , Schema della strategia di profilazione. I circuiti NeuroFEM su Loihi 2 sono stati eseguiti in due modalità: transitoria (in alto) e a stato stazionario (in basso). In modalità transitoria, il bias veniva invertito di segno ogni 4.096 intervalli temporali (un’epoca di soluzione), costringendo la rete a fluire verso una nuova soluzione. In modalità stazionaria, il bias rimaneva costante, mantenendo la rete nel suo regime di attivazione stazionario per l’intera esecuzione. Confrontando la differenza di energia e tempo tra le due modalità, abbiamo potuto stimare l’energia e il tempo richiesti da ciascuna epoca di soluzione.
d , L’errore relativo rispetto alla soluzione analitica per le soluzioni generate da Loihi 2 e le soluzioni convenzionali. La natura a punto fisso di Loihi 2 porta a prestazioni peggiori rispetto alle simulazioni CPU di NeuroFEM, ma le prestazioni non crescono in modo eccessivo nell’intervallo di risoluzioni della mesh testate. L’implementazione di Loihi 2 della mesh a più bassa risoluzione e di 16 neuroni per nodo della mesh non convergeva in modo affidabile, probabilmente a causa delle instabilità introdotte dalla conversione a punto fisso e del loro effetto sproporzionato su un circuito così piccolo. Le barre di errore mostrano la media ± deviazione standard su dieci esecuzioni separate.
e , L’errore relativo tra le soluzioni generate da Loihi 2 e le soluzioni convenzionali. Le curve sono in gran parte simili a
d perché le soluzioni convenzionali sono già vicine alla soluzione analitica. Le barre di errore mostrano la media ± deviazione standard su dieci esecuzioni separate.
f , Energia totale richiesta da ciascun modello NeuroFEM per 131.072 intervalli temporali in funzione della risoluzione della mesh, dei neuroni per nodo della mesh e della modalità di esecuzione. Le barre di errore indicano la media ± deviazione standard su quattro esecuzioni separate.
g , La differenza di energia per epoca di soluzione per modelli NeuroFEM con 8 o 16 neuroni per nodo della mesh. Le barre di errore indicano la media ± deviazione standard.
h , Il tempo di esecuzione per epoca di soluzione in funzione della risoluzione della mesh, dei neuroni per nodo della mesh e della modalità di esecuzione. Le barre di errore indicano la media ± deviazione standard
. i, La differenza di tempo di esecuzione per epoca di soluzione per modelli NeuroFEM con 8 o 16 neuroni per nodo mesh. Le barre di errore indicano la media ± deviazione standard
Questa scelta introduce inevitabilmente differenze rispetto a una simulazione floating-point: gli errori aumentano, ma il punto è che restano stabili con la dimensione del problema oltre certe soglie. Vengono descritte deviazioni relative medie e massime che, pur superiori al caso ideale, non portano a divergenze. È qui che il discorso si sposta dal “perfetto” al “utilizzabile”: se l’errore rimane confinato, prevedibile e gestibile, l’hardware neuromorfo diventa un candidato per classi di problemi dove energia e parallelismo contano più della precisione ultra-fine, oppure dove si può compensare con mesh più dense, averaging più lungo o calibrazione dei parametri.
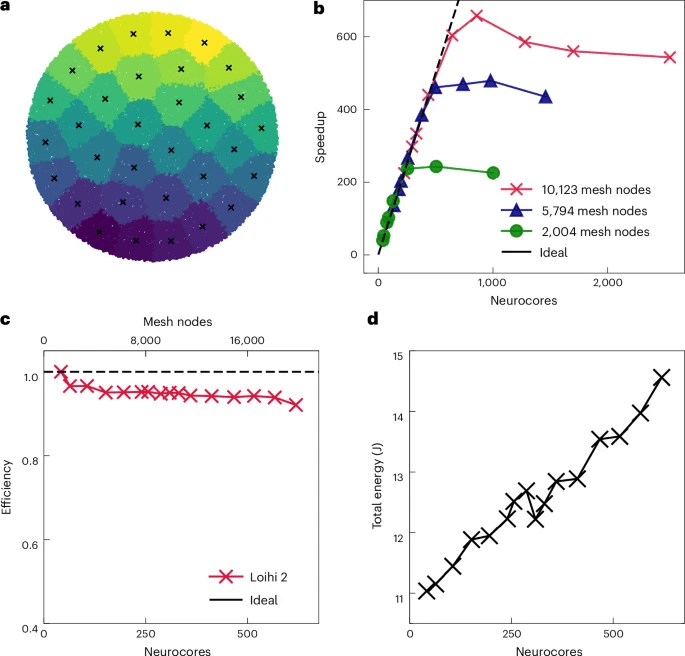
b , Un forte ridimensionamento di NeuroFEM mostra prestazioni di ridimensionamento ideali fino a diverse centinaia di core per modelli di dimensioni fisse. Oltre questo punto, i guadagni di ridimensionamento diminuiscono in conformità con la legge di Amdahl, poiché il modello diventa troppo piccolo per utilizzare efficacemente i core aggiuntivi.
c , Un debole ridimensionamento di NeuroFEM mostra un’efficienza quasi ideale quando le dimensioni del modello aumentano con il numero di core.
d , Un debole ridimensionamento di NeuroFEM multi-chip si traduce in un modesto aumento del consumo energetico totale a un tasso inferiore a 1, suggerendo una maggiore efficienza energetica su larga scala. Tutte le simulazioni sono state eseguite su tutti i 32 chip per 131.072 intervalli temporali.
C’è un altro dettaglio che merita attenzione: alcune configurazioni, come aumentare neuroni per nodo oltre certe soglie su mesh piccole, possono rendere instabile il sistema. È una lezione tipica dei sistemi dinamici: più complessità non significa automaticamente più stabilità. Significa più gradi di libertà, che vanno controllati. In un solutore neuromorfo, questo controllo avviene attraverso parametri che ricordano più una progettazione di circuito che una scelta di tolleranze numeriche.
Energia e scaling: perché il neuromorfo diventa interessante solo quando cresce
Il vantaggio promesso dal neuromorfo non è un “benchmark” su un problema singolo. È il comportamento quando si scala. Loihi 2, grazie a comunicazioni asincrone e al fatto che gli spike sono eventi discreti, riduce il costo della comunicazione rispetto a modelli sincroni. La conseguenza è che, se la mappatura mantiene costante il numero di sinapsi per neurone al crescere della mesh, la rete conserva una proprietà di scalabilità che in altri paradigmi si degrada.
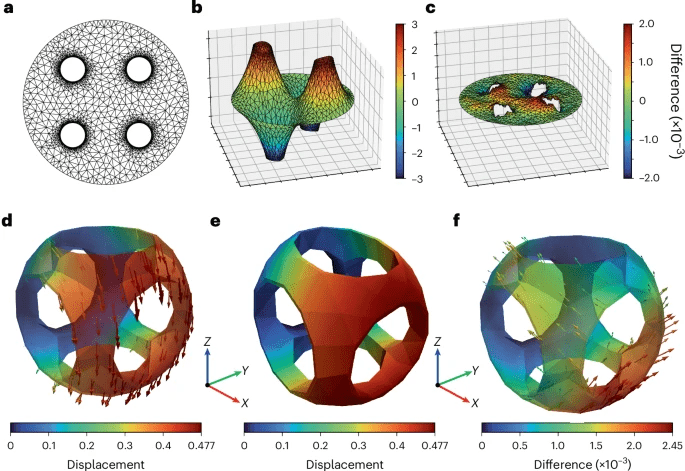
b , Soluzione generata da NeuroFEM per l’equazione di Poisson sulla mesh topologicamente non banale con condizioni al contorno di Dirichlet sul contorno esterno e condizioni al contorno di Neumann sui bordi dei fori interni.
c , La differenza tra la soluzione NeuroFEM in
b e la soluzione convenzionale. Le differenze sono limitate in grandezza da 2 × 10
−3 .
d , Soluzione NeuroFEM alle equazioni di elasticità lineare su una mesh tetraedrica (3D) topologicamente non banale soggetta a una densità di forza di volume costante (gravità) nella direzione -Z
. La faccia -X
è fissa in posizione e le restanti facce sono libere. La soluzione è ora un campo vettoriale anziché un campo scalare.
e , Come
d ma con i vettori di spostamento applicati come una deformazione della mesh originale. La soluzione concorda con l’aspettativa del cedimento del solido cavo sotto gravità.
f , La differenza tra la soluzione NeuroFEM e una soluzione convenzionale. Le ampiezze dei vettori differenza sono limitate da 2,45 × 10
−3 .
I profili energetici descritti parlano di epoche di soluzione forzate tramite inversione dei bias e di energia extra che scala linearmente con il numero di nodi, con picchi nell’ordine di 80 millijoule per epoca. Il tempo extra cresce anch’esso in modo lineare fino a decine di millisecondi in esempi riportati, mentre il grado di parallelizzabilità stimato è estremamente alto, tale da rendere lo scaling forte “idealmente” sostenibile fino a fattori molto elevati, compatibilmente con limiti di I/O e scheduling. Il confronto con solutori CPU come GMRES e CG viene interpretato soprattutto sul fronte energia: la CPU può essere competitiva in tempo su certe configurazioni, ma paga più in joule, mentre lo scenario neuromorfo mantiene il consumo molto basso a parità di problema risolto. Il risultato è che il vantaggio cresce con la scala: più il problema diventa “grande e sparso”, più l’architettura event-driven evita sprechi.
Dal laboratorio al “neuromorphic twin”: soluzioni che cambiano in tempo reale
Il passaggio più visionario, ma anche più plausibile, è l’idea di usare una rete NeuroFEM come “twin” neuromorfo collegato a sensori esterni. Se un sistema fisico cambia e il termine noto o le condizioni al contorno variano, la rete potrebbe aggiornare bias e parametri a runtime e convergere verso una nuova soluzione senza ripartire da zero. Questo non sostituisce un simulatore HPC, ma crea una categoria diversa: un solutore che vive vicino al sistema fisico, consuma poco, e restituisce stime continue. È un modello compatibile con applicazioni dove conta la risposta rapida più della precisione assoluta: manutenzione predittiva, controllo strutturale, robotica, simulazioni che devono restare in-loop con dati reali. In queste aree, la crisi energetica del computing non è una teoria: è una limitazione quotidiana. E l’hardware neuromorfo, se riesce davvero a mappare metodi numerici consolidati senza chiedere alla community di reinventare tutto, potrebbe ritagliarsi uno spazio dove oggi dominano soluzioni costose e spesso sovradimensionate. Il punto finale, forse il più importante, è culturale: NeuroFEM non chiede di credere in una nuova magia. Chiede di prendere il FEM, che è uno standard industriale e scientifico, e di farlo vivere su un hardware che assomiglia al cervello nella cosa che più conta per l’energia: comunicare solo quando serve.
Iscriviti alla Newsletter
Non perdere le analisi settimanali: Entra nella Matrice Digitale.
Matrice Digitale partecipa al Programma Affiliazione Amazon EU. In qualità di Affiliato Amazon, ricevo un guadagno dagli acquisti idonei. Questo non influenza i prezzi per te.









