Nel computing quantistico c’è una verità scomoda che molti roadmap tendono a nascondere dietro medie e benchmark: le prestazioni reali di un processore dipendono dai qubit peggiori. Non dai migliori, non dalla media, non dal caso ideale. Dipendono da quelli che degradano senza preavviso, che passano da “stabili” a “instabili” nel giro di pochi millisecondi e che trasformano una macchina da laboratorio in un sistema capriccioso, difficile da calibrare e ancora più difficile da scalare. La scoperta annunciata da un team danese, pubblicata su Physical Review X, mette il dito proprio lì: non solo dimostra che queste fluttuazioni possono essere tracciate in tempo reale, ma lo fa a una velocità circa 100 volte superiore rispetto ai metodi precedenti, rendendo finalmente “osservabile” un fenomeno che finora veniva spesso smussato da misure lente e mediate. Il cuore del risultato è un sistema adattivo che misura e aggiorna costantemente la stima di decadimento di un qubit, riuscendo a vedere quando un qubit cambia stato di affidabilità in una finestra temporale coerente con la velocità stessa del fenomeno. Non è una semplice ottimizzazione incrementale. È un cambio di paradigma: invece di raccogliere dati per minuti o ore e calcolare una media, il sistema entra in una logica di diagnostica continua, dove ogni nuova misura modifica l’ipotesi corrente e spinge subito l’esperimento nella direzione più informativa. Questo, in laboratorio, significa una cosa molto concreta: passare da “capire che un qubit è problematico dopo ore” a capirlo in secondi, con statistiche sufficienti per isolare cause, correlazioni e pattern.
Il problema che blocca la scalabilità: qubit che “saltano” e materiali che si muovono
La parte più interessante del lavoro non è solo la velocità. È ciò che la velocità consente di osservare. Il team descrive difetti materiali microscopici che si spostano centinaia di volte al secondo, producendo fluttuazioni rapide e imprevedibili nei parametri del qubit. È una frase che va letta bene: non stiamo parlando di rumore astratto, ma di una dinamica fisica concreta, in cui piccole imperfezioni nel materiale o nell’interfaccia cambiano posizione o stato e alterano il comportamento del qubit con una frequenza tale da rendere inutili molte misurazioni tradizionali, perché troppo lente per inseguire il fenomeno. Quando misuri lentamente, ottieni una media che sembra “accettabile”. Ma quella media maschera un comportamento intermittente: un qubit che per una frazione di tempo è buono e subito dopo diventa cattivo. Dal punto di vista di un processore quantistico, questo è devastante, perché gli algoritmi e la correzione d’errore non vivono nelle medie: vivono nella consistenza operativa, nella capacità di mantenere un certo livello di coerenza e di tassi di rilassamento in modo prevedibile.
È qui che il lavoro danese si inserisce come strumento di verità: se puoi vedere la transizione “buono-cattivo” in millisecondi, allora puoi smettere di raccontarti che quel qubit “va bene in media” e iniziare a progettare per ciò che fa davvero.
Il salto tecnico: dal computer “lento” all’FPGA che chiude il loop
Il motivo per cui questa misurazione diventa 100 volte più veloce non è magia, è architettura. Il team utilizza un controller FPGA commerciale, indicato come OPX1000 di Quantum Machines, per eseguire aggiornamenti adattivi direttamente vicino all’hardware sperimentale. Questo dettaglio è decisivo perché aggira un collo di bottiglia classico: la latenza del trasferimento dati verso un computer convenzionale, dove analizzi, calcoli, decidi il passo successivo e poi rimandi comandi allo strumento.
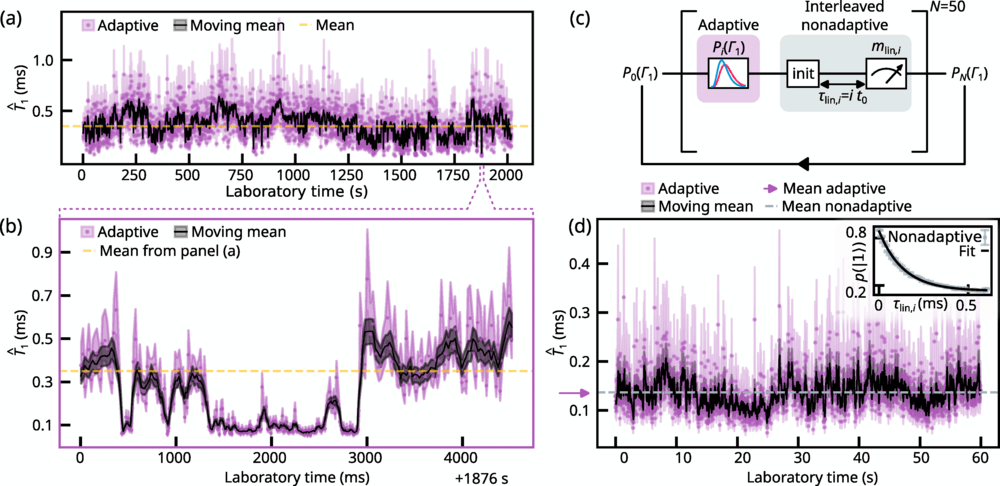
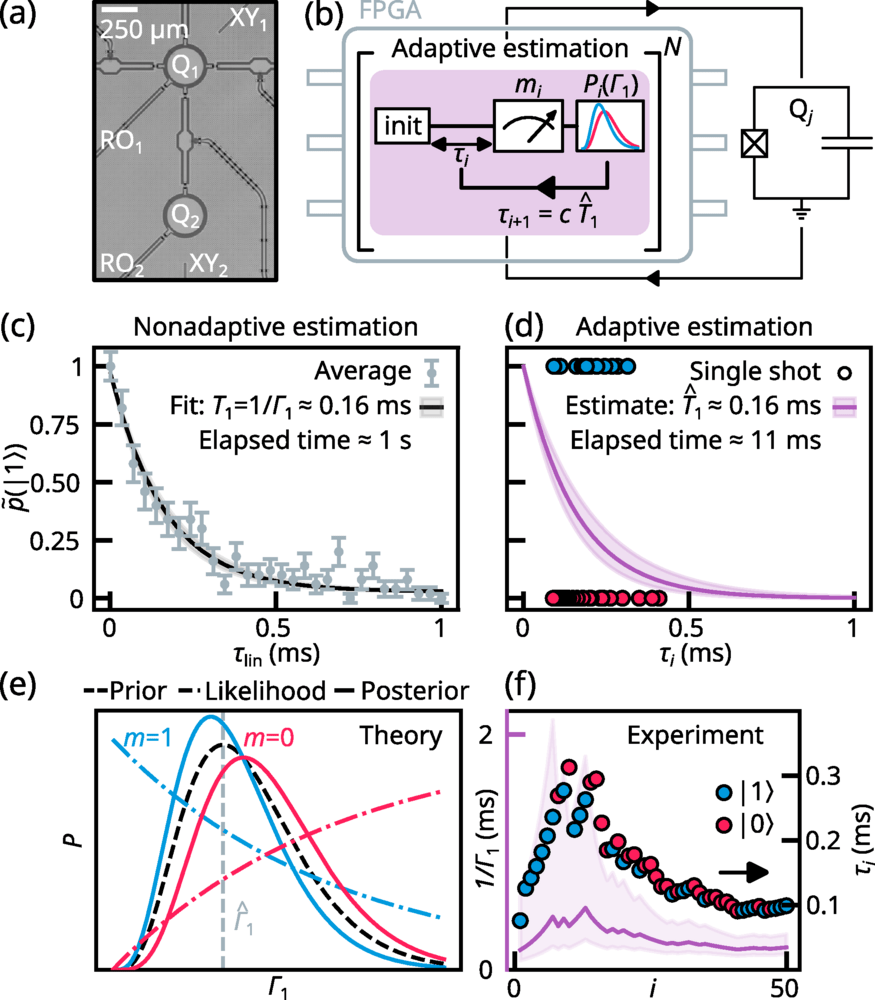
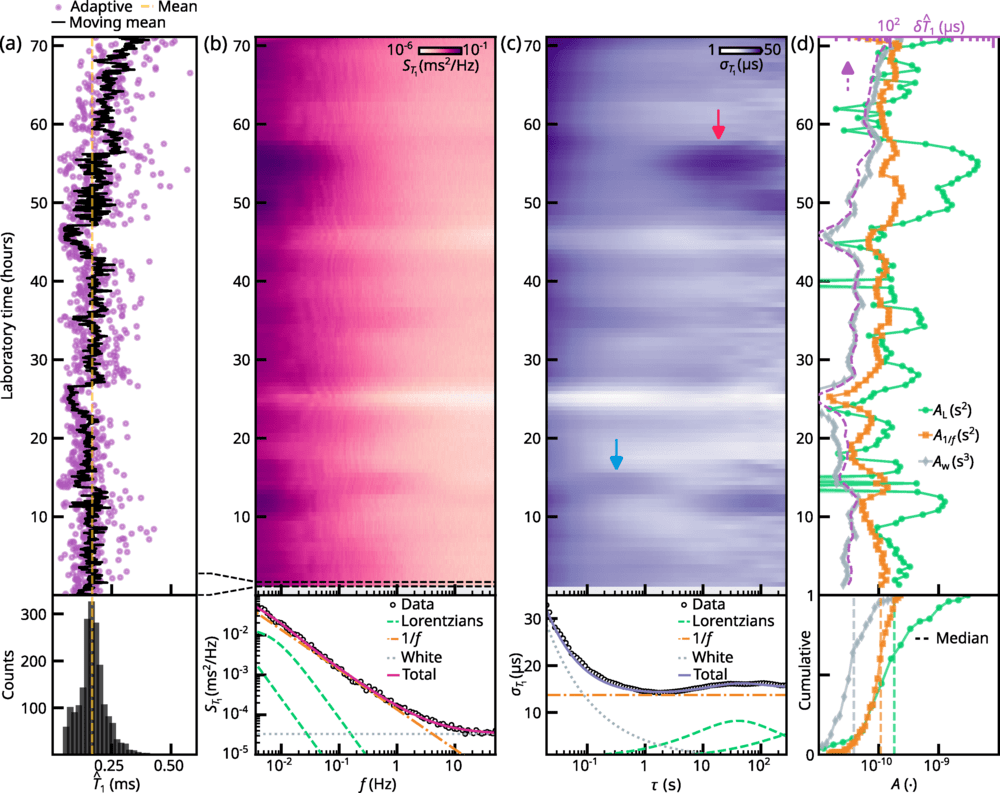
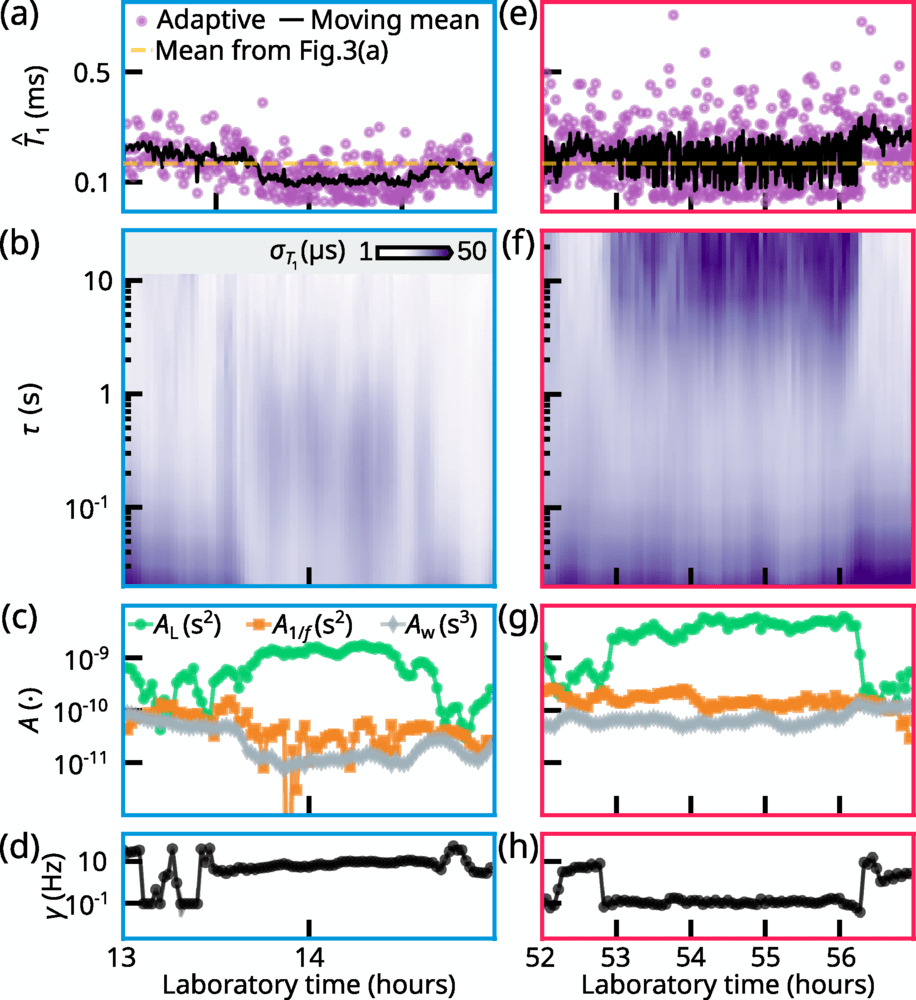
^𝑇1(punti viola, sottocampionati da 𝐷 =30) e il suo intervallo di credibilità del 68% (area ombreggiata). Ogni punto viola in questo grafico ha richiesto un tempo medio di stima di ≈20 MSLa linea gialla tratteggiata indica il valore medio di tutte le stime ¯𝑇1 ≈350 μSLa linea nera è una media mobile su 100 campioni e l’area ombreggiata nera è il suo intervallo di confidenza del 68% (vedere il testo principale). (b) Stimato ^𝑇 1A ≈1876 Sdel pannello (a) (vedi linee tratteggiate viola), dove ^𝑇 1mostra la commutazione telegrafica con scale temporali dell’ordine di decine o centinaia di millisecondi. (c) La sequenza di stima interlacciata per 𝛤1utilizzato per convalidare il protocollo adattivo. Ciascuno dei 𝑁cicli di sonda, etichettati 𝑖, è costituito da parti che contribuiscono alle stime adattive (viola) e non adattive (grigio). Ogni ciclo di sonda adattiva è seguito dalla parte non adattiva del ciclo, in cui il qubit viene nuovamente inizializzato nello stato eccitato, il tempo di attesa è fissato a 𝜏lioN,𝑖 =𝑖𝜏0e il risultato della misurazione viene memorizzato per la post-elaborazione offline. Dopo l’ 𝑁cicli di sonda, la distribuzione finale ottenuta in modo adattivo 𝒫𝑁(𝛤1)viene salvato. (d) Risultati sperimentali per il protocollo di tracciamento adattivo, intervallati da misurazioni non adattive. Pannello principale: La stima ^𝑇 1(punti viola) e intervallo di credibilità del 68% (area ombreggiata) corrispondente alla distribuzione di probabilità finale 𝒫50(𝛤1)delle 2000 stime adattive eseguite durante il ≈60 Sdell’esperimento. La linea nera mostra una media mobile su 5 campioni e l’area ombreggiata in nero è il suo intervallo di confidenza del 68%. La freccia viola indica la media di tutte le stime adattive. ^𝑇 1La linea tratteggiata è il valore estratto dall’adattamento mostrato nel riquadro. Riquadro: Risultati sperimentali per la stima non adattiva utilizzando il tempo di attesa campionato linearmente 𝜏lioN,𝑖Le barre di errore rappresentano l’errore standard.
Quel ping-pong funziona per esperimenti lenti. Non funziona quando i qubit fluttuano “alla velocità del fenomeno”. L’FPGA, invece, permette di chiudere il loop: misura, aggiorna il modello, decide la prossima impostazione, misura di nuovo. Tutto su un tempo compatibile con la fisica che stai inseguendo. In pratica, è come passare da un controllo manuale a un controllo in tempo reale. E nel quantistico, dove i dettagli contano e i tempi contano di più, questo significa poter fare diagnostica “sulla dinamica”, non sul ricordo.
L’idea chiave: aggiornamento bayesiano dopo ogni misura
La seconda metà della svolta è matematica e metodologica: l’uso di modelli bayesiani che aggiornano una “best guess” dopo ogni singola misurazione. È un approccio che, nel contesto, ha una conseguenza enorme: non ti serve accumulare un grande batch di dati prima di prendere decisioni sperimentali. Ti basta iniziare con poche misure, costruire una stima iniziale e poi farla evolvere mentre misuri. Questa logica adattiva permette di concentrare lo sforzo sperimentale sui punti più informativi. Se un qubit sta cambiando comportamento, l’algoritmo lo “vede” perché la distribuzione delle stime si allarga o si sposta rapidamente. Se invece è stabile, lo conferma senza consumare tempo in misure ridondanti.
Nel racconto che hai fornito, questo si traduce in un risultato operativo netto: raccogliere statistiche su qubit problematici in secondi invece che in ore. E in un laboratorio dove il tempo di calibrazione può divorare giorni, ridurre questo lavoro a finestre brevi non è solo comodità. È capacità di iterazione, e quindi velocità di progresso.
Perché conta: la performance di un processore è definita dal qubit peggiore
C’è un passaggio che vale come tesi editoriale: il sistema quantistico viene limitato dal suo anello più debole. Nei processori classici, un core “peggiore” si gestisce con scheduling e ridondanza. Nel quantistico, il qubit instabile è un punto di rottura. Le architetture di correzione d’errore, che sono l’unica strada realistica verso macchine utili, richiedono uniformità e prevedibilità. Se una parte del chip entra e esce da uno stato di affidabilità, l’intero schema deve compensare, e compensare significa aumentare overhead, aumentare qubit di supporto, aumentare complessità.
Quindi, quando il team dice che serve “capire i qubit cattivi”, sta dicendo che serve smettere di ottimizzare solo i qubit già buoni e iniziare a fare ingegneria su ciò che degrada. È un cambio di priorità che, se adottato industrialmente, può accelerare la transizione da prototipi impressionanti a sistemi realmente scalabili. In altre parole, la scoperta non “aumenta la coerenza” per magia. Aumenta la capacità di trovare il motivo per cui la coerenza crolla.
Il valore industriale: hardware commerciale, integrazione rapida e un ecosistema europeo
Il lavoro sottolinea anche un elemento che interessa l’industria: l’uso di hardware commerciale come acceleratore. Quando una tecnica dipende da elettronica custom e irripetibile, resta spesso confinata. Quando invece sfrutta un controller FPGA già presente in un ecosistema di laboratorio, diventa più facile replicarla, confrontarla, integrarla nelle pipeline di calibrazione. La presenza di Quantum Machines come fornitore chiave suggerisce un trend più ampio: il quantistico sta costruendo un middle layer industriale, fatto di controller, stack di controllo, tool di programmazione e automazione, senza cui la scalabilità resta teoria. Nel quadro che riporti compaiono anche collaborazioni tra istituti scandinavi e olandesi, oltre alla fabbricazione del chip in un contesto come Chalmers University. È un dettaglio importante perché indica che non siamo davanti a un esperimento isolato, ma a un tentativo di rendere la metodologia robusta su più infrastrutture e più filiere di fabbricazione. E nel quantistico, dove la riproducibilità è spesso il vero ostacolo, la rete di validazione conta quasi quanto il risultato.
Cosa cambia in laboratorio: dalla media che maschera al monitoraggio che rivela
Con metodi tradizionali, spesso si misura un parametro del qubit su un tempo lungo, si ottiene un numero medio e lo si usa per calibrare. Ma se il qubit fluttua rapidamente, quella calibrazione è una fotografia sfocata. Il qubit può comportarsi bene durante la misura e male durante l’esecuzione, o viceversa. La conseguenza è un sistema che sembra “a posto” e poi fallisce. Il monitoraggio in tempo reale, invece, rende possibile distinguere tra qubit stabilmente buoni e qubit intermittenti. E soprattutto permette di vedere se un qubit passa da uno stato all’altro in una finestra breve. Questo crea due possibilità: o si interviene sul controllo e sul scheduling per evitare di usare quel qubit nei momenti peggiori, o si usa la diagnostica per risalire alla causa fisica e migliorare materiali e processi. È qui che la scoperta diventa ponte tra fisica e ingegneria: non si limita a dire “c’è rumore”. Dice “c’è rumore dinamico” e ti dà lo strumento per tracciarlo.
Implicazioni per il futuro: stabilizzare i superconduttori prima di inseguire i numeri
Il lavoro si applica a qubit superconduttori, oggi uno dei pilastri industriali del settore. La sfida per renderli utili non è solo aumentare il numero di qubit su chip. È garantire che quel numero sia composto da qubit sufficientemente uniformi da sostenere correzione d’errore e algoritmi non dimostrativi. Se la fisica dei difetti continua a produrre fluttuazioni rapide, aumentare la scala senza risolvere la dinamica significa solo aumentare l’instabilità complessiva. Questa tecnica, invece, porta una prospettiva pragmatica: prima di inseguire record, bisogna costruire strumenti che rendano l’instabilità misurabile e quindi affrontabile. È un passo che spesso manca nelle narrazioni “da corsa quantistica”, dove si parla di scaling come se fosse solo una questione di fabbricazione e di layout, e non anche di microfisica dei materiali. E qui torna l’idea più concreta: se riesci a identificare in tempo reale quando un qubit passa da stabile a instabile, puoi smettere di trattare l’instabilità come un dato “misterioso” e iniziare a trattarla come un parametro di progetto.
Iscriviti alla Newsletter
Non perdere le analisi settimanali: Entra nella Matrice Digitale.
Matrice Digitale partecipa al Programma Affiliazione Amazon EU. In qualità di Affiliato Amazon, ricevo un guadagno dagli acquisti idonei. Questo non influenza i prezzi per te.








