La possibilità di comprendere, prevedere e stabilizzare sistemi dinamici complessi rappresenta una delle sfide centrali della scienza contemporanea. Dalla fisica dei sistemi non lineari alla climatologia, dall’ingegneria meccanica alla neuroscienza, la difficoltà non risiede più nella scarsità di dati, ma nella capacità di estrarre rappresentazioni dinamiche interpretabili da osservazioni sperimentali grezze, spesso ad alta dimensionalità e fortemente non lineari. In questo contesto si inserisce il lavoro dei ricercatori della Duke University, che propongono un framework data-driven capace di derivare modelli lineari a bassa dimensionalità direttamente dai dati sperimentali, abilitando un’analisi globale automatica delle dinamiche del sistema.
Il risultato non è un semplice miglioramento predittivo, ma un cambio di paradigma: il modello appreso non si limita a replicare traiettorie osservate, bensì ricostruisce una struttura latente lineare interpretabile, coerente con la teoria dell’operatore di Koopman, in grado di fornire garanzie empiriche di stabilità, scoprire autofunzioni e identificare set invarianti complessi.
Cosa leggere
Dalla teoria dei sistemi dinamici al problema dei dati reali
La teoria dei sistemi dinamici fornisce da oltre un secolo un quadro matematico potente per descrivere fenomeni evolutivi in domini scientifici estremamente diversi. Tuttavia, l’applicazione di questa teoria a sistemi reali resta profondamente problematica. I modelli analitici richiedono una conoscenza dettagliata delle equazioni governanti, mentre i sistemi osservabili nel mondo reale sono spesso affetti da non linearità forti, rumore, dimensionalità elevata e accoppiamenti non noti.
Il risultato è una frattura storica tra teoria e pratica. Da un lato, strumenti teorici eleganti ma applicabili solo a modelli ideali; dall’altro, approcci puramente data-driven che sacrificano interpretabilità e stabilità per ottenere buone prestazioni locali. Il lavoro della Duke University tenta di ricomporre questa frattura, mostrando che è possibile apprendere rappresentazioni coordinate lineari globali anche per sistemi dinamici non lineari complessi, partendo esclusivamente da dati sperimentali.
Koopman, linearità globale e rappresentazioni latenti
Il fondamento teorico di questo approccio affonda le radici nel lavoro di Bernard Koopman del 1931, che dimostrò come qualunque sistema dinamico non lineare possa essere descritto come lineare in uno spazio di funzioni infinite dimensionali. In questo formalismo, l’evoluzione temporale non agisce sugli stati, ma sulle osservabili del sistema, tramite un operatore lineare.
Il problema storico di questo approccio è duplice. Da un lato, lo spazio di Koopman è in generale infinito dimensionale; dall’altro, l’identificazione pratica delle autofunzioni rilevanti è estremamente complessa. Gran parte della ricerca recente si è concentrata su metodi approssimati come la Dynamic Mode Decomposition e le sue estensioni, che tuttavia producono rappresentazioni ad alta dimensionalità, spesso ridondanti e difficilmente interpretabili.
Il framework proposto dalla Duke University compie un passo ulteriore: dimostra che, con le giuste scelte architetturali e di regolarizzazione, è possibile apprendere embedding lineari a bassa dimensionalità che catturano la struttura globale della dinamica, mantenendo al contempo accuratezza predittiva e interpretabilità.
Embedding time-delay e informazione mutua
Uno degli elementi chiave del framework è l’uso sistematico dell’embedding time-delay come ingresso del modello. Questo approccio, ben noto nella teoria dei sistemi dinamici, permette di ricostruire lo spazio delle fasi a partire da osservazioni parziali, sfruttando il fatto che la storia temporale di un sistema contiene informazione sufficiente sulla sua dinamica interna.
La novità non risiede nell’uso del time-delay in sé, ma nella selezione automatica della lunghezza del delay tramite informazione mutua. Invece di fissare arbitrariamente il numero di ritardi, gli autori analizzano la dipendenza informativa tra le traiettorie per individuare una dimensione di embedding che massimizzi il contenuto informativo senza introdurre ridondanza.
Questa scelta preliminare si rivela cruciale per garantire stabilità numerica, generalizzazione predittiva e parsimonia del modello, soprattutto quando si lavora con dati sperimentali rumorosi e sistemi non completamente osservabili.
Autoencoder profondi informati dalla fisica
Al cuore del framework si trova una rete autoencoder profonda, progettata non come semplice strumento di compressione non lineare, ma come meccanismo di apprendimento di coordinate dinamiche fisicamente coerenti. Lo spazio latente non è libero di organizzarsi arbitrariamente, ma viene vincolato a evolvere secondo un modello dinamico lineare.
Durante l’addestramento, l’encoder mappa gli stati time-delayed in uno spazio latente a bassa dimensionalità. In questo spazio, la dinamica è descritta da un sistema lineare appreso. Il decoder ricostruisce poi gli stati originali a partire dalle previsioni latenti. Questo schema costringe il modello a scoprire una rappresentazione in cui la complessità non lineare del sistema è assorbita nella trasformazione di coordinate, lasciando la dinamica effettiva lineare.
La scelta di imporre linearità nello spazio latente non è un vincolo arbitrario, ma una dichiarazione epistemologica: se il modello riesce a prevedere correttamente a lungo orizzonte con una dinamica lineare a bassa dimensionalità, allora quella rappresentazione contiene una descrizione essenziale del sistema.
Previsioni a lungo orizzonte e annealing del fattore di sconto
Uno dei problemi principali nei modelli data-driven per sistemi dinamici è la degradazione rapida delle previsioni nel tempo. Molti modelli ottengono buoni risultati su orizzonti brevi, ma divergeno rapidamente quando vengono iterati. Gli autori affrontano questo problema introducendo una strategia di curriculum learning basata su annealing del fattore di sconto.
Durante l’addestramento, il modello viene supervisionato non solo sulla previsione immediata, ma su rollout predittivi multipli nel futuro. Ogni previsione futura è pesata da un fattore di sconto gamma, che inizialmente privilegia gli orizzonti brevi e viene progressivamente annealed per includere orizzonti sempre più lunghi.
Questa strategia consente al modello di imparare dinamiche globalmente coerenti, migliorando la generalizzazione di quasi due ordini di grandezza rispetto ad approcci a orizzonte fisso. Il risultato è una capacità predittiva che si estende ben oltre l’orizzonte di addestramento, prerequisito fondamentale per qualunque analisi di stabilità affidabile.
Scoperta automatica di autofunzioni e set invarianti
Una volta addestrato, il modello fornisce molto più di semplici previsioni. Poiché la dinamica nello spazio latente è lineare, è possibile analizzarla tramite strumenti classici dell’algebra lineare. Le autofunzioni di Koopman emergono direttamente come combinazioni lineari degli stati latenti, rendendo accessibili strutture dinamiche altrimenti nascoste.
Questo permette di identificare attrattori, cicli limite, bacini di attrazione e set invarianti in modo automatico, senza imporre a priori una struttura al sistema. Inoltre, la presenza di una dinamica lineare consente di costruire funzioni di Lyapunov empiriche, fornendo garanzie di stabilità globale basate sui dati.
Questa capacità rappresenta uno dei contributi più rilevanti del lavoro: la stabilità non viene più dedotta da un modello analitico ideale, ma inferita empiricamente da una rappresentazione appresa che generalizza correttamente nel tempo.
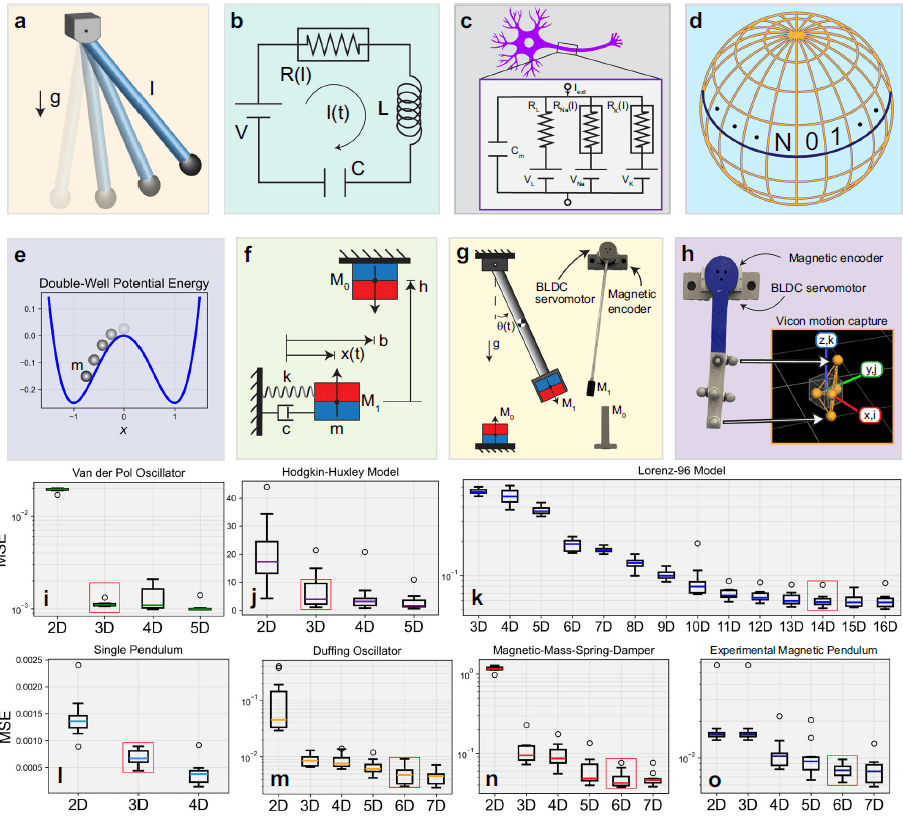
Sistemi studiati: dal pendolo al caos atmosferico
Gli autori validano il framework su nove dataset che coprono un ampio spettro di comportamenti dinamici. I sistemi più semplici includono il pendolo singolo, descritto efficacemente da una rappresentazione lineare tridimensionale, nonostante la sua dinamica non lineare intrinseca. Anche in questo caso, l’aggiunta di dimensioni latenti oltre le tre non produce miglioramenti significativi, confermando la parsimonia della rappresentazione appresa.
Sistemi più complessi come l’oscillatore di Van der Pol e l’oscillatore di Duffing vengono modellati accuratamente con rappresentazioni rispettivamente 3D e 6D. In entrambi i casi, il modello cattura cicli limite e fenomeni di multistabilità, riducendo drasticamente la comparsa di modi spurii tipici di approcci ad alta dimensionalità.
Particolarmente significativo è l’uso del framework su sistemi storicamente difficili, come il modello di Hodgkin-Huxley per l’eccitazione neuronale e il sistema Lorenz-96 per la dinamica atmosferica. In questi casi, il modello riesce a estrarre coordinate latenti che preservano la struttura dinamica globale, pur partendo da dati ad alta dimensionalità e fortemente accoppiati.
Dati sperimentali e validazione nel mondo reale
Un elemento distintivo del lavoro è l’enfasi sui dati sperimentali reali, non limitandosi a simulazioni ideali. Gli autori applicano il framework a pendoli magnetici sperimentali e a sistemi meccanici con multistabilità indotta, dimostrando che l’approccio mantiene robustezza anche in presenza di rumore, incertezze di misura e dinamiche non modellate.
Questo aspetto è cruciale per la trasferibilità del metodo. Il framework non richiede una conoscenza preliminare delle equazioni del sistema, né una scelta manuale delle coordinate. Tutto il processo, dalla selezione del delay all’analisi di stabilità, è automatizzato e data-driven, rendendo l’approccio applicabile a contesti in cui la modellazione analitica è impraticabile.
Implicazioni per fisica, clima e ingegneria
Le implicazioni di questo lavoro sono ampie. In fisica, il framework offre un nuovo strumento per esplorare sistemi non lineari complessi senza imporre modelli semplificati. Nella scienza del clima, la possibilità di derivare rappresentazioni dinamiche lineari a bassa dimensionalità potrebbe migliorare la comprensione della prevedibilità a lungo termine. In ingegneria, l’identificazione automatica di set invarianti e regioni stabili apre nuove prospettive per il controllo e la progettazione di sistemi resilienti.
Più in generale, il lavoro suggerisce che la scelta delle coordinate giuste è il vero problema centrale nell’analisi dei sistemi dinamici. Il deep learning, quando guidato da vincoli fisici e da una struttura teorica solida, può diventare uno strumento di scoperta scientifica, non solo di approssimazione numerica.
Un passo verso l’analisi automatica globale
Il framework sviluppato alla Duke University rappresenta un passo concreto verso un’analisi globale automatica delle dinamiche sperimentali. Non promette soluzioni universali, ma dimostra che è possibile integrare teoria dei sistemi dinamici, apprendimento profondo e dati reali in un’unica architettura coerente.
In un’epoca in cui la complessità dei sistemi supera spesso la capacità di modellazione umana diretta, questo approccio indica una direzione chiara: non semplificare il sistema, ma scoprire rappresentazioni che rendano la complessità analizzabile. È una prospettiva che potrebbe ridefinire il modo in cui scienza e ingegneria affrontano i sistemi dinamici nel mondo reale.
