Un gruppo internazionale di ricercatori introduce una rivoluzione nella modellistica predittiva: i predittori lineari di massimo accordo (MALP) e la loro versione stimata (EMALP). Questi modelli superano i limiti dei metodi di regressione classica, ponendo al centro non la minimizzazione dell’errore, ma il massimo accordo statistico tra predizioni e valori osservati, misurato attraverso il coefficiente di correlazione di concordanza (CCC). Lo studio, che confronta MALP con i tradizionali predittori ai minimi quadrati (ELSLP), mostra come la nuova metodologia migliori la coerenza e la concordanza nei dati, soprattutto in contesti biostatistici e clinici dove la precisione relativa è più importante dell’errore medio assoluto.
Cosa leggere
Fondamenti teorici dei predittori MALP
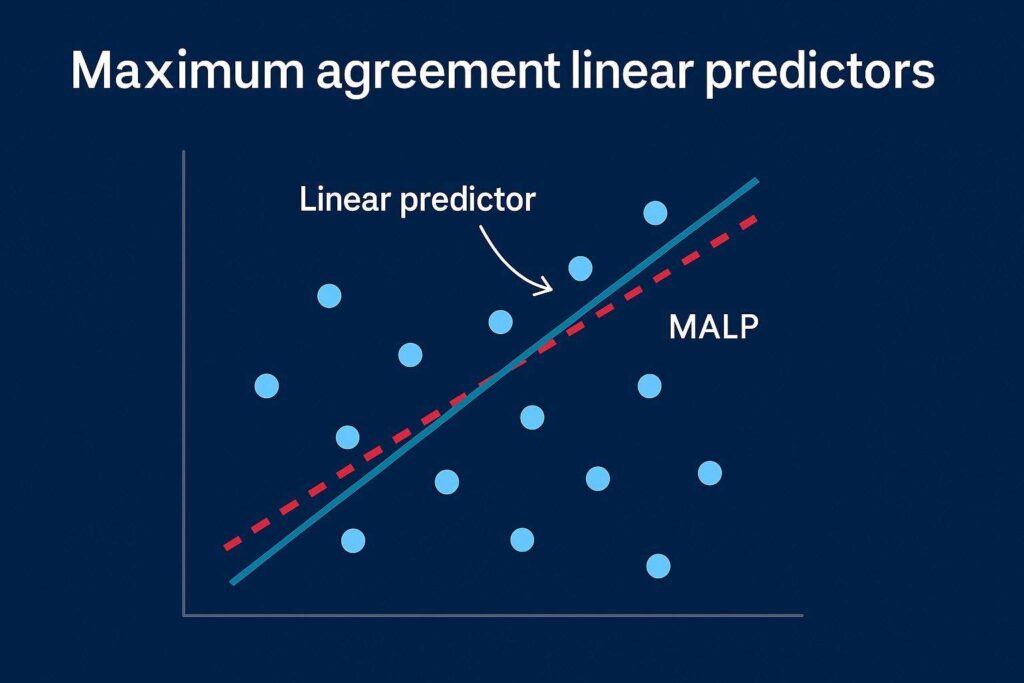
Il MALP viene definito come la funzione lineare che massimizza il coefficiente di concordanza tra predittore e predittando, un indice che misura simultaneamente precisione e accuratezza lungo la linea di perfetto accordo a 45 gradi. In questo quadro, il MALP risulta essere una trasformazione lineare del predittore ai minimi quadrati (LSLP), centrata e scalata per eguagliare media e varianza del valore osservato. In casi univariati, il MALP coincide con la regressione geometrica media o la regressione dell’asse maggiore ridotto, ma gli autori estendono il concetto a covariate multidimensionali, mantenendo la stessa efficienza computazionale. Le dimostrazioni teoriche provano che, per distribuzioni normali, il massimo CCC corrisponde al coefficiente di correlazione multipla, creando un legame diretto tra i modelli di regressione classici e questa nuova visione orientata all’accordo. La ricerca riprende riferimenti storici come il coefficiente intraclasse e i diagrammi di Bland-Altman, evidenziando la debolezza del coefficiente di Pearson (PCC) nel misurare l’accordo reale. Gli autori integrano e generalizzano i lavori precedenti di Bottai, estendendo la teoria a casi in cui i parametri non sono noti e devono essere stimati. Le proprietà di consistenza forte vengono dimostrate tramite le leggi dei grandi numeri, mentre la normalità asintotica emerge dal teorema del limite centrale multivariato.
Proprietà asintotiche e intervalli di confidenza
Il modello EMALP, basato su stime campionarie, possiede proprietà asintotiche che lo rendono utilizzabile in contesti applicativi complessi. Gli autori dimostrano che EMALP converge a una distribuzione normale asintotica, con varianza derivata tramite il metodo delta. Sotto ipotesi di normalità multivariata, tali varianze assumono forme chiuse che semplificano la costruzione di intervalli di confidenza e di predizione. Le simulazioni computazionali mostrano che gli intervalli asintotici e jackknife offrono buoni livelli di copertura per campioni medi, mentre i metodi bootstrap risultano meno affidabili per campioni piccoli o correlazioni deboli. L’analisi evidenzia che, sebbene gli intervalli MALP siano più ampi di quelli LSLP a causa della maggiore variabilità, garantiscono maggior accordo complessivo tra le predizioni e i valori osservati. Gli autori propongono correzioni di bias e trasformazioni di Fisher per migliorare la stabilità inferenziale, suggerendo dimensioni minime del campione per evitare distribuzioni bimodali quando la correlazione è prossima allo zero. Questi risultati offrono una base solida per applicazioni pratiche in cui l’accordo statistico prevale sulla mera accuratezza numerica.
Studi empirici e prestazioni comparative
Tre esperimenti computazionali dimostrano la superiorità del modello EMALP nel massimizzare il CCC rispetto all’approccio tradizionale ELSLP. Nel primo, i ricercatori verificano la bontà delle approssimazioni asintotiche per media e varianza, confermando l’accuratezza per correlazioni superiori a 0,5 e campioni oltre 30 osservazioni. Nel secondo, EMALP ottiene valori di concordanza superiori, pur con un errore quadratico medio (MSE) leggermente più alto, e identici coefficienti di Pearson rispetto ai metodi classici. Nel terzo esperimento, gli autori testano la normalità campionaria in contesti non gaussiani, confermando la robustezza dell’approccio. Le simulazioni mostrano che EMALP produce cluster di punti stretti lungo la diagonale di perfetto accordo, rendendolo particolarmente adatto in ambiti dove la riproducibilità clinica è essenziale.
Applicazioni reali e validazione empirica
L’applicazione dei metodi a dati reali ne conferma la validità. Nel primo caso, relativo a un set di dati oculistici con 46 osservazioni, EMALP viene utilizzato per predire lo spessore maculare da misure OCT, ottenendo un CCC superiore rispetto a ELSLP. Nel secondo, su un dataset di composizione corporea con 252 osservazioni, il modello predice la percentuale di grasso corporeo basandosi su misure antropometriche come peso e circonferenza addominale. I risultati mostrano che l’aggiunta di più predittori migliora l’accordo ma porta a rendimenti decrescenti, suggerendo la necessità di criteri di selezione basati sulla complessità del modello. Le tabelle riassuntive e i grafici dimostrano che EMALP fornisce stime più coerenti con la distribuzione osservata, rendendolo preferibile nei contesti medici e sperimentali. Un pacchetto R dedicato implementa le funzioni di stima, visualizzazione e calcolo degli intervalli, facilitando l’adozione immediata del metodo da parte dei ricercatori.
Prospettive e sviluppi futuri
Il lavoro apre nuove linee di ricerca sul tema dell’accordo statistico. Gli autori propongono un’estensione del CCC aggiustato per il numero di predittori, analogamente all’R² aggiustato nei modelli di regressione. Altri sviluppi riguardano la costruzione di test d’ipotesi per i coefficienti MALP, la regolarizzazione in scenari ad alta dimensionalità e l’integrazione in framework di machine learning ibrido, dove l’accordo tra predizioni può migliorare la stabilità dei modelli. Questa prospettiva sposta l’attenzione dall’errore alla concordanza effettiva, una metrica più rilevante nei settori clinici, biostatistici e nelle scienze dei dati. Il MALP e il suo stimatore EMALP rappresentano così una svolta concettuale: non semplici strumenti di regressione, ma predittori di armonia statistica, capaci di catturare il vero grado di accordo tra modelli e realtà.
