L’elaborazione dei tensori nelle reti neurali entra in una fase di transizione storica grazie al nuovo paradigma POMMM, una soluzione che realizza la moltiplicazione matrice–matrice attraverso un’unica propagazione coerente della luce, eliminando le limitazioni fisiche ed energetiche dei tradizionali calcolatori digitali. Questa architettura ottica consente di eseguire CNN, Vision Transformer e operazioni complesse come multi-head self-attention con un livello di parallelismo impossibile da ottenere con GPU o con le precedenti architetture fotoniche. Il lavoro pubblicato su Nature Photonics evidenzia come la combinazione tra proprietà bosoniche della luce, trasformate ottiche e modulazioni di fase permetta di costruire un processo computazionale universale, estremamente scalabile e compatibile con le infrastrutture software esistenti. L’avanzamento rappresenta un passo decisivo verso un calcolo neurale a bassissimo consumo, ad altissima velocità e con capacità di esecuzione diretta dei modelli moderni, senza stratagemmi di multiplexing né modifiche strutturali ai modelli addestrati su GPU.
Cosa leggere
Limiti attuali del calcolo neurale digitale
Le reti neurali moderne impongono un peso computazionale enorme alle infrastrutture digitali. La maggior parte delle operazioni che compongono il training e l’inferenza viene eseguita sotto forma di MMM, che richiedono trasferimenti di memoria costanti e un uso intensivo dei tensor core delle GPU. Questo comporta un consumo energetico elevatissimo e una saturazione della banda di memoria, elementi che rappresentano un collo di bottiglia critico nel calcolo AI su larga scala. Le tecniche ottiche finora sviluppate hanno proposto soluzioni alternative, come VMM, calcolo per diffrazione o combinazioni fase-ampiezza. Tuttavia, queste architetture hanno richiesto più passaggi ottici, o hanno introdotto compromessi che limitano la generalità del calcolo. Il risultato è un panorama fotonico frammentato, efficace solo per operazioni specifiche ma incapace di gestire l’intera pipeline di una rete neurale moderna. Il paradigma POMMM interviene su questo nodo critico introducendo una logica computazionale che permette di realizzare tutti i prodotti scalari necessari all’MMM in parallelo, utilizzando un singolo processo fisico e senza artifici esterni. Il sistema rompe quindi il compromesso tra parallelismo e generalità che ha caratterizzato la ricerca ottica negli ultimi anni.
Concetto e funzionamento del POMMM
Il cuore del POMMM si basa sulle proprietà fondamentali della luce: superposizione, linearità, duale spaziale-frequenziale, shift invariance. Le matrici da moltiplicare vengono codificate direttamente sull’onda ottica attraverso modulazioni di ampiezza e di fase. Le righe della prima matrice vengono distinte tramite gradienti di fase specifici, mentre la seconda matrice viene inserita in forma trasposta con modulazione di ampiezza. A questo punto, l’esecuzione del prodotto scalare tra righe e colonne, normalmente distribuita su migliaia di operazioni digitali, viene compressa in una singola trasformazione ottica: una trasformata di Fourier colonnare che permette alla luce di eseguire simultaneamente e senza interferenze tutti i dot product tra le righe di A e le colonne di B.
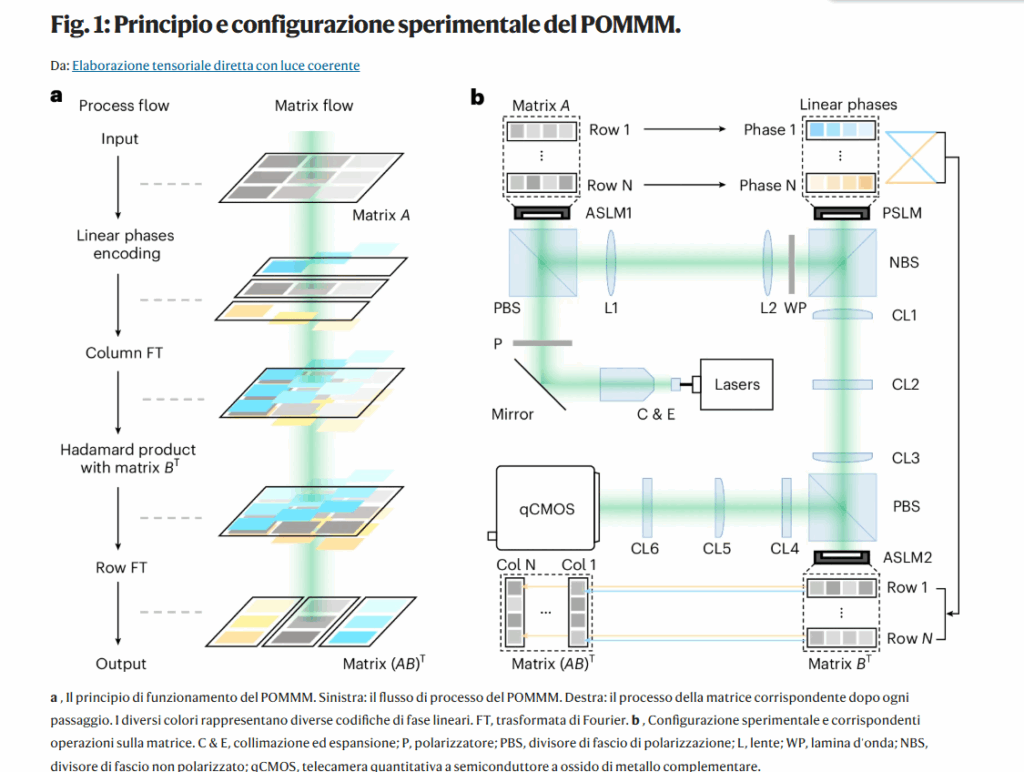
La luce, propagando attraverso i modulatori e le lenti, realizza così le fasi dell’MMM: moltiplicazione degli elementi, accumulo delle somme e posizionamento risultante nella matrice finale. L’intera matrice C = A × B emerge fisicamente nella distribuzione del campo luminoso catturata dalla fotocamera ad alta risoluzione.
Simulazioni e dimostrazione sperimentale
Gli autori validano il paradigma attraverso simulazioni teoriche e un prototipo ottico completo. Le simulazioni coinvolgono tre modelli di propagazione: FFT, Huygens–Fresnel e Rayleigh–Sommerfeld, ottenendo coerenza elevata tra i modelli e con i risultati sperimentali. Il prototipo utilizza una sorgente laser, due modulatori spaziali di luce per ampiezza e fase, un set di lenti per implementare la trasformazione ottica e una camera qCMOS per acquisire l’output.
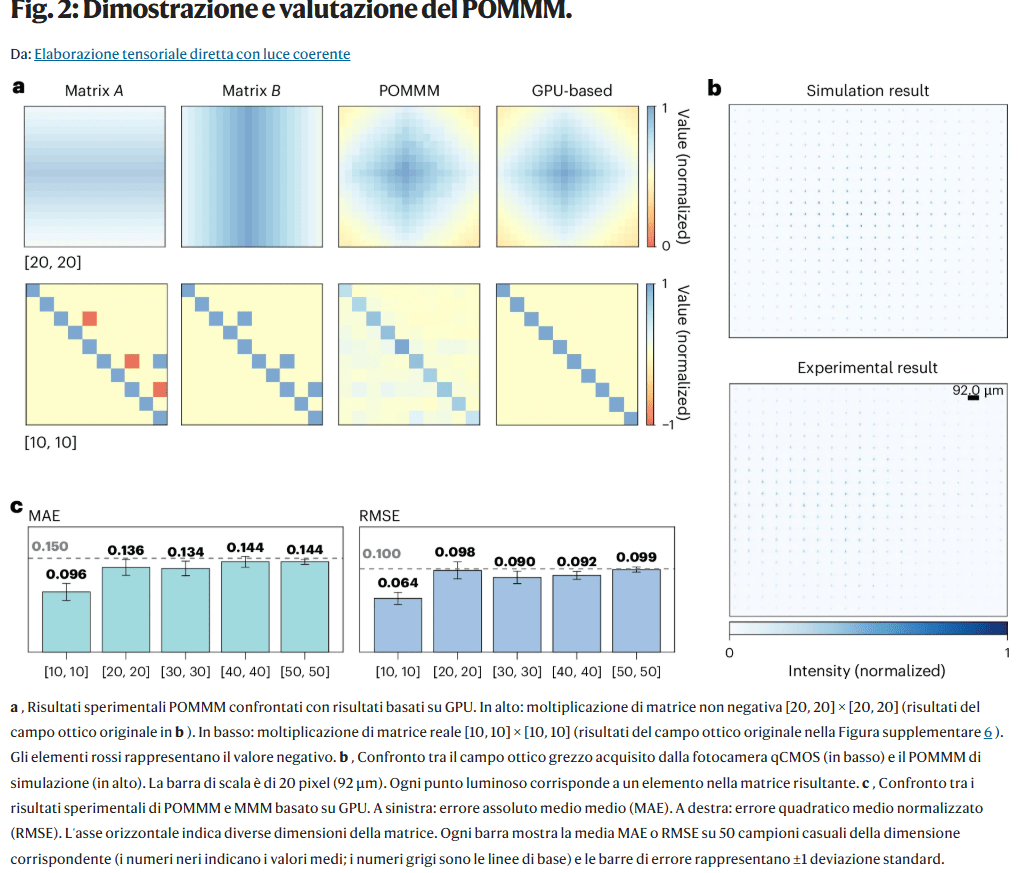
I risultati mostrano una corrispondenza quasi perfetta con l’MMM eseguita da GPU, confermando che il calcolo avviene correttamente anche su matrici di dimensioni crescenti. Questo elemento è essenziale per trasferire direttamente modelli neurali GPU sul sistema ottico senza adattamenti.
Implementazione ottica di CNN
Il paradigma viene applicato a una intera rete convoluzionale, dimostrando che ogni operazione convoluzionale può essere reinterpretata come un MMM. Una convoluzione multi-canale, tradotta in forma matriciale, diventa una serie di operazioni che POMMM può eseguire in un singolo passaggio. L’immagine viene scomposta in finestre, ogni finestra viene trasformata in vettore e moltiplicata per il kernel tramite MMM ottica. L’output convoluzionale viene quindi appiattito e passato a un livello fully connected anch’esso implementato attraverso il sistema ottico.
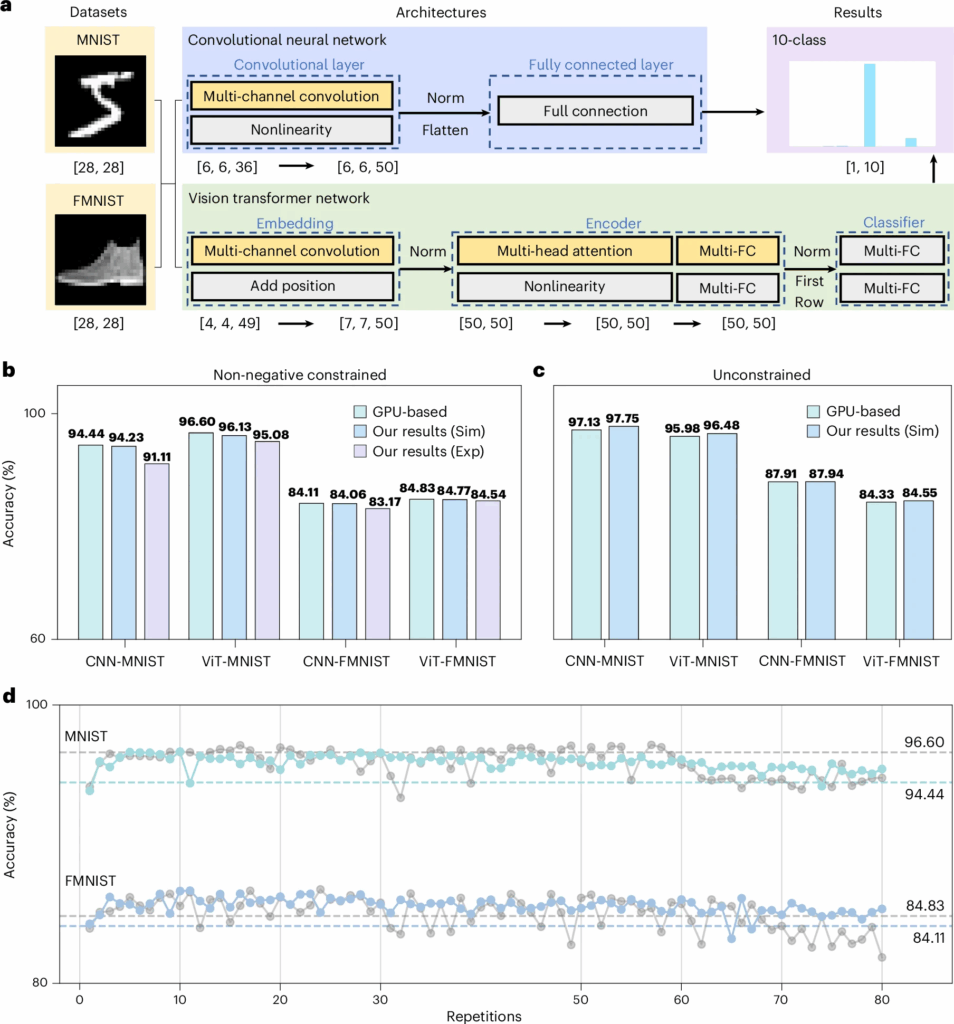
b , Test di distribuzione diretta di pesi addestrati tramite GPU con vincoli non negativi su diverse reti e set di dati su simulazione e prototipo POMMM (le matrici di confusione sono mostrate nella Figura
12 supplementare ). Sim, simulazione; Exp, esperimento.
c , Test di distribuzione diretta di pesi addestrati tramite GPU senza vincoli a tutti i passaggi su diversi set di dati su simulazione POMMM (le matrici di confusione sono mostrate nella Figura
15 supplementare ).
d , Confronto dell’accuratezza dell’inferenza ONN basata su POMMM con diversi errori di calcolo (relativi alle ripetizioni degli elementi). Le curve colorate sono modelli CNN, le curve grigie sono modelli ViT e le linee tratteggiate sono la baseline corrispondente dei modelli non negativi basati su GPU. Immagini
riprodotte con autorizzazione da: in alto, rif.
47 con licenza Creative Commons
CC BY-SA 3.0 ; in basso, rif.
50 © 2017 Zalando SE.
Le prove su MNIST e Fashion-MNIST mostrano che la rete ottica può replicare fedelmente la pipeline GPU, mantenendo qualità e consistenza nel processo di classificazione. La dimostrazione evidenzia la possibilità di trasformare intere CNN in pipeline ottiche con consumi energetici estremamente ridotti.
Vision Transformer ottico e self-attention fisica
Una delle parti più avanzate dello studio riguarda la realizzazione ottica di un Vision Transformer, un modello che si basa su un uso intensivo della moltiplicazione matrice–matrice per generare query, key e value. Tutte queste operazioni vengono implementate tramite POMMM. L’embedding dei patch avviene tramite convoluzione ottica, mentre la self-attention sfrutta il prodotto triplo QK T V, che diventa naturalmente eseguibile in forma ottica.
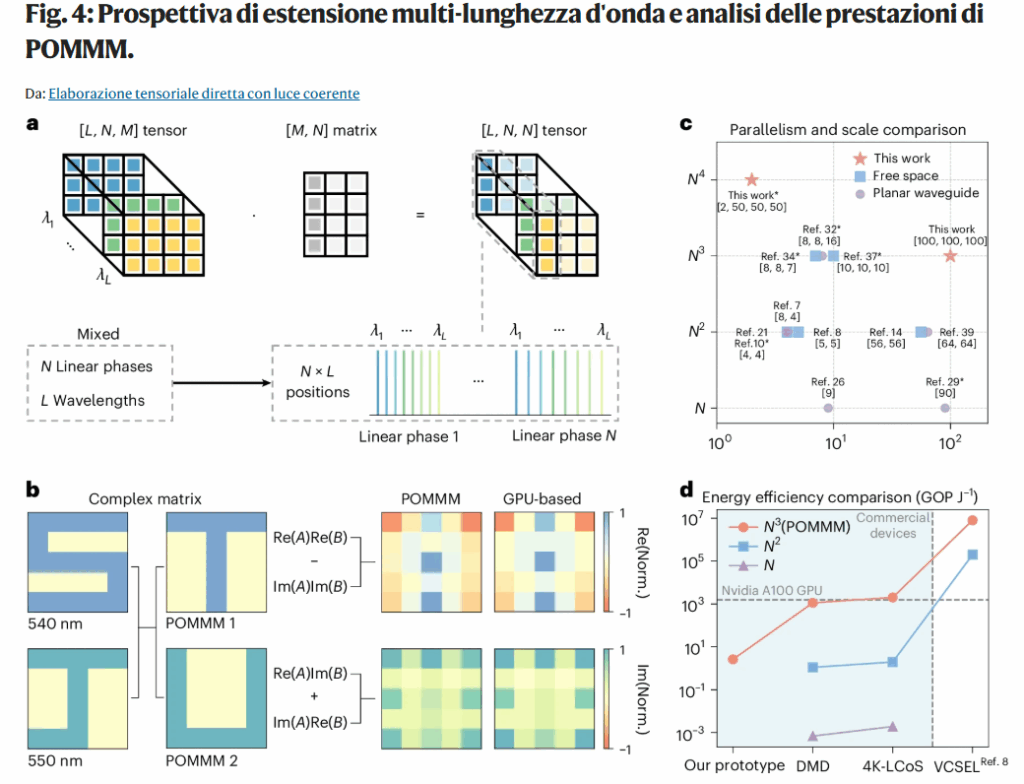
b , Dimostrazione del multiplexing di lunghezza d’onda di POMMM mediante due matrici complesse. Norm., normalizzazione. ‘S’ e ‘J’ sono rispettivamente le parti reale e immaginaria della matrice complessa
A , che vengono modulate a lunghezze d’onda di 540 nm e 550 nm. Dopo il multiplexing di due lunghezze d’onda di POMMM, eseguono rispettivamente la moltiplicazione tensore-matrice con la parte reale ‘T’ e la parte immaginaria ‘U’ della matrice complessa
B per ottenere una matrice complessa completa (i risultati intermedi e i campi ottici originali sono mostrati nella Figura
17 supplementare ).
c , Potenza di calcolo teorica confrontata con i paradigmi di calcolo ottico esistenti (Tabella supplementare
1 ). L’asterisco indica il multiplexing multi-lunghezza d’onda. L’asse verticale rappresenta il parallelismo computazionale single-shot (
N i indica che la complessità temporale richiesta a una piattaforma digitale per eseguire questo calcolo è O(
N i )), mentre l’asse orizzontale indica la scala computazionale effettiva raggiunta negli esperimenti (indicata dalla dimensione più piccola).
d , Valutazione pratica dell’efficienza energetica. DMD, dispositivo digitale a microspecchi; LCoS, cristalli liquidi su silicio; VCSEL, laser a emissione superficiale a cavità verticale; GOP J
− 1 , giga (10
9 ) operazioni per Joule. L’asse verticale indica l’efficienza energetica e l’asse orizzontale rappresenta diverse piattaforme di dispositivi. Ogni curva corrisponde a un paradigma computazionale con un livello specifico di potenza di calcolo teorica. Il punto dati all’estrema sinistra indica le prestazioni effettive del nostro prototipo (nella Tabella supplementare
2 ), mentre tutti gli altri valori sono stimati in condizioni ideali (ovvero, pieno utilizzo del dispositivo, nella Tabella supplementare
3 ).
Il sistema produce token di classe e rappresentazioni interne compatibili con la pipeline ViT classica. Questo dimostra che il calcolo ottico può gestire i modelli più avanzati oggi utilizzati nell’intelligenza artificiale, comprese strutture complesse per cui il costo computazionale digitale è estremamente elevato.
Scalabilità del modello ottico
Il POMMM non si limita alle operazioni elementari, ma esplora la scalabilità attraverso differenti dimensioni di matrici, differenti formati dati e l’utilizzo di multi-wavelength multiplexing, che permette di eseguire simultaneamente più MMM sfruttando lunghezze d’onda diverse. Questo approccio aggiunge un ulteriore ordine di parallelismo, senza aumentare il tempo di propagazione. La capacità di gestire operazioni su larga scala rende il paradigma adatto a modelli con milioni o miliardi di parametri. Inoltre, l’architettura può estendersi tramite matrici di modulatori più ampie, aumentare la profondità del calcolo o distribuire la propagazione su sistemi ottici paralleli, convertendo la naturale espansione fisica della luce in ulteriore capacità computazionale.
Confronto con i paradigmi ottici precedenti
Lo studio distingue nettamente il POMMM dagli approcci precedenti, evidenziando che non richiede:
propagazioni multiple
multiplexing spazio-tempo
precomputazioni inverse
architetture basate interamente su diffrazione
Il risultato è un modello di calcolo universale, capace di integrare in maniera nativa qualsiasi operazione MMM, mantenendo compatibilità con modelli progettati per GPU. Il calcolo ottico non diventa più una soluzione settoriale, ma un acceleratore general-purpose.
Implicazioni per il futuro del calcolo AI
Il paradigma POMMM introduce una prospettiva profondamente diversa sul calcolo neurale. Le reti profonde, che oggi consumano enormi quantità di energia, potrebbero essere eseguite tramite processi ottici con consumi ridotti di ordini di grandezza e con velocità prossime ai limiti fisici della propagazione luminosa. L’integrazione con pipeline GPU permette la creazione di sistemi ibridi che sfruttano la potenza del silicio per operazioni non lineari e quella della luce per le fasi lineari dei modelli neurali. Il POMMM segna un passaggio verso un computing AI in cui la luce svolge il ruolo principale nell’elaborazione dei tensori e in cui il calcolo digitale diventa solo una componente di supporto. L’idea che un’intera architettura neurale possa essere elaborata in un singolo passaggio ottico per layer proietta l’AI in una dimensione completamente nuova, modellata dalla fisica e non più dai transistor.
